Устная олимпиада "Открытие"
5-7 класс (май 2010 года)
Задачи
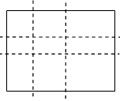
Задача 1. Частички прямоугольника
Прямоугольный лист разрезают по горизонтальным и вертикальным линиям, идущим вдоль сторон листа. В результате лист поделился на несколько прямоугольных частей. Пример показан на рисунке справа.
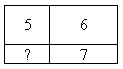
(а) На рисунке снизу показано одно такое деление. Про три прямоугольника указали их периметры. Найдите периметр четвертой части.
|
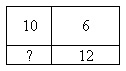
(б) На рисунке снизу показано одно такое деление. Про три прямоугольника указали их площади. Найдите площадь четвертой части.
|
Пусть прямоугольник поделен на 4 части, как и в пунктах (a) и (б).
(в) Периметры трех частей составляют целое число сантиметров.
Верно ли, что периметр самого прямоугольника составляет целое число сантиметров?
(г) Площади трех частей составляют целое число квадратных сантиметров.
Верно ли, что площадь самого прямоугольника составляет целое число квадратных сантиметров?
Пусть прямоугольник поделен четырьмя горизонтальными и четырьмя вертикальными линиями на 25 частей. Будем называть прямоугольник «хорошим», если её периметр составляет целое число сантиметров.
(д) Известно, что 21 частей — хорошие.
Верно ли, что весь прямоугольник (который делили на части) — хороший?
(е) Известно, что 21 частей — хорошие.
Верно ли, что все остальные части тоже хорошие?
Задача 2. Фокусы экстрасенса
Перед экстрасенсом лежит колода из 36 карт рубашкой вверх, то есть ему не видна масть карт. Он называет масть верхней карты и открывает её. Потом называет масть второй карты и открывает её. И так далее. Экстрасенс пытается угадать масть как можно большего числа карт.
(а) Как экстрасенсу угадать масть 9 карт?
Рубашка карты показана на рисунке справа. Она не симметричная. У экстрасенса есть помощник. Он знает порядок карт в колоде, не может менять этот порядок. Но может расположить рубашку колоды так, как хочет.
Как договориться экстрасенсу и помощнику, чтобы экстрасенс мог угадать масть
(б) каких-то 18 карт,
(в) каждой второй карты (второй, четвертой, …, 36-ой),
(г) каких-то 19 карт,
(д) каких-то 20 карт,
(е) более чем 20 карт?
Задача 3. Доказательства на суде
На суде в качестве вещественного доказательства предъявлено несколько монет.
Суд же знает только то, что фальшивые монеты весят одинаково, настоящие монеты весят одинаково и что фальшивые монеты легче настоящих. Суд не знает, сколько монет являются настоящими.
Эксперт выяснил про каждую монету, настоящая она или фальшивая. Оказалось, что фальшивых монет ровно половина. В распоряжении эксперта — чашечные весы без гирь.
(а) Пусть всего 6 монет. Как за 2 взвешивания предъявить суду (с доказательством) все 3 фальшивые монеты?
(б) Пусть всего 6 монет. Как за 2 взвешивания предъявить суду (с доказательством) все 3 фальшивые и 3 настоящих?
(в) Пусть всего 14 монет. Как менее чем за 7 взвешиваний предъявить суду (с доказательством) все 7 фальшивых монет?
(г) Пусть всего 14 монет. Как за 3 взвешивания предъявить суду (с доказательством) все 7 фальшивых монет?
(д) Пусть всего 14 монет. Как за 3 взвешивания предъявить суду (с доказательством) все 7 фальшивых монет и 7 настоящих?
(е) Пусть всего 62 монеты. Как за 5 взвешивания предъявить суду (с доказательством) все 31 фальшивую монету и 31 настоящую?
| 
